Trigonometric Functions in a Right Triangle
Solved Problems
Example 1.
Given the right triangle below, find the values of \(\sin \alpha,\) \(\cos \alpha,\) \(\tan \alpha,\) \(\cot \alpha,\) \(\sin \beta,\) \(\cos \beta,\) \(\tan \beta,\) and \(\cot \beta.\)
Solution.
First we find the length of the hypotenuse using the Pythagorean theorem . Let \(a = 5,\) \(b = 12.\) Then
\[{a^2} + {b^2} = {c^2},\;\; \Rightarrow c = \sqrt {{a^2} + {b^2}} = \sqrt {{5^2} + {{12}^2}} = \sqrt {25 + 144} = \sqrt {169} = 13.\]
Using the trigonometric ratios in a right triangle, we have
\[\begin{array}{*{20}{l}}
{\sin \alpha = \frac{a}{c} = \frac{5}{{13}},} &{\cos \alpha = \frac{b}{c} = \frac{{12}}{{13}},}\\[1em]
{\tan \alpha = \frac{a}{b} = \frac{5}{{12}},} &{\cot \alpha = \frac{b}{a} = \frac{{12}}{{5}},}\\[1em]
{\sin \beta = \frac{b}{c} = \frac{12}{{13}},} &{\cos \beta = \frac{a}{c} = \frac{{5}}{{13}},}\\[1em]
{\tan \beta = \frac{b}{a} = \frac{12}{{5}},} &{\cot \beta = \frac{a}{b} = \frac{{5}}{{12}}.}
\end{array}\]
Example 2.
Evaluate the six trigonometric functions of the angle \(\alpha\) shown in the figure.
Solution.
Using the Pythagorean theorem , we find the second leg of the right triangle. Let \(b = 12,\) \(c = 15.\) Then
\[{a^2} + {b^2} = {c^2},\;\; \Rightarrow a = \sqrt {{c^2} - {b^2}} = \sqrt {{{15}^2} - {{12}^2}} = \sqrt {225 - 144} = \sqrt {81} = 9.\]
Calculate the trigonometric functions:
\[\begin{array}{*{20}{l}}
{\sin \alpha = \frac{a}{c} = \frac{9}{{15}} = \frac{3}{5},} &{\cos \alpha = \frac{b}{c} = \frac{{12}}{{15}} = \frac{4}{5},}\\[1em]
{\tan \alpha = \frac{a}{b} = \frac{9}{{12}} = \frac{3}{4},} &{\cot \alpha = \frac{b}{a} = \frac{{12}}{{9}} = \frac{4}{3},}\\[1em]
{\sec \alpha = \frac{c}{b} = \frac{15}{{12}} = \frac{5}{4},} &{\csc \alpha = \frac{c}{a} = \frac{{15}}{{9}} = \frac{15}{3}.}
\end{array}\]
Example 3.
What is the value of \(\tan 45^\circ?\)
Solution.
Consider an isosceles right triangle.
Figure 5. It has equal legs \(a = b,\) and each of the acute angles of the triangle is equal to \(45^\circ.\) Therefore
\[\require{cancel}\tan {45^\circ} = \frac{a}{b} = \frac{\cancel{a}}{\cancel{a}} = 1.\]
Example 4.
What is the value of \(\cot 30^\circ?\)
Solution.
Consider a \(30\text{-}60\text{-}90\) triangle, which is a special right triangle whose angles are \(30^\circ,\) \(60^\circ,\) and \(90^\circ.\)
Figure 6. In any \(30\text{-}60\text{-}90\) triangle, the hypotenuse is twice as long as the shortest leg, so \(c = 2a.\)
Using this property together with the Pythagorean theorem, we express the other leg \(b\) in terms of \(a:\)
\[{a^2} + {b^2} = {c^2},\;\; \Rightarrow b = \sqrt {{c^2} - {a^2}} = \sqrt {{{\left( {2a} \right)}^2} - {a^2}} = \sqrt {4{a^2} - {a^2}} = \sqrt {3{a^2}} = a\sqrt 3 .\]
Now we can calculate the value of \(\cot 30^\circ :\)
\[\cot {30^0} = \frac{b}{a} = \frac{{\cancel{a}\sqrt 3 }}{\cancel{a}} = \sqrt 3 .\]
Example 5.
Calculate the value of \(\sec 45^\circ.\)
Solution.
In an isosceles right triangle, the legs are equal to each other, that is \(a = b.\) Then by the Pythagorean theorem,
\[c = \sqrt {{a^2} + {b^2}} = \sqrt {{a^2} + {a^2}} = \sqrt {2{a^2}} = a\sqrt 2 .\]
The secant of an angle of \(45^\circ\) is given by
\[\sec {45^\circ} = \sec \alpha = \frac{c}{b} = \frac{{\cancel{a}\sqrt 2 }}{\cancel{a}} = \sqrt 2 .\]
Example 6.
Calculate the value of \(\csc 30^\circ.\)
Solution.
In a \(30\text{-}60\text{-}90\) triangle, the length of the hypotenuse is twice the length of the shortest leg. Hence \(c = 2a,\) where the side \(a\) is opposite to the angle \(\alpha = 30^\circ.\)
Find \(\csc 30^\circ:\)
\[\csc {30^\circ} = \frac{c}{a} = \frac{{2\cancel{a}}}{\cancel{a}} = 2.\]
Example 7.
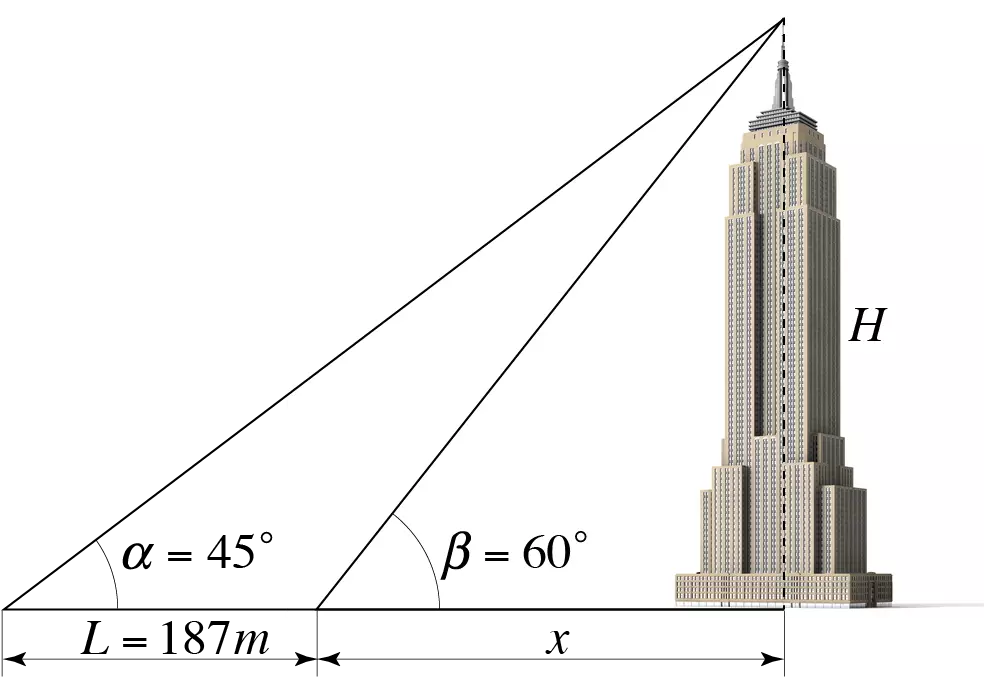
To determine the height of the Empire State Building, two measurements are taken. At the initial point, the angle of elevation to the top of the building is \(\alpha = 45^\circ.\) After moving closer by \(L = 187\,m,\) the angle of elevation is \(\beta = 60^\circ.\) Find the height \(H\) of the building.
Solution.
Figure 7. Let \(x\) be the distance from the terminal point to the building. Then the initial distance is equal to \(L + x.\) Using the trigonometric ratios for the right triangles shown in the figure, we get two equations:
\[\left\{ \begin{array}{l}
H = \left( {L + x} \right)\tan \alpha \\
H = x\tan \beta
\end{array} \right..\]
Solve this system to express \(H\) in terms of \(L, \alpha, \text{and } \beta.\)
\[\left\{ \begin{array}{l}
H = \left( {L + x} \right)\tan \alpha \\
H = x\tan \beta
\end{array} \right.,\;\; \Rightarrow \left\{ \begin{array}{l}
H = L\tan \alpha + x\tan \alpha \\
H = x\tan \beta
\end{array} \right.,\;\; \Rightarrow \left\{ \begin{array}{l}
x\tan \beta = L\tan \alpha + x\tan \alpha \\
H = x\tan \beta
\end{array} \right.,\;\; \Rightarrow \left\{ \begin{array}{l}
x\left( {\tan \beta - \tan \alpha } \right) = L\tan \alpha \\
H = x\tan \beta
\end{array} \right.,\;\; \Rightarrow \left\{ \begin{array}{l}
x = \frac{{L\tan \alpha }}{{\tan \beta - \tan \alpha }}\\
H = x\tan \beta
\end{array} \right.,\;\; \Rightarrow H = \frac{{L\tan \alpha \tan \beta }}{{\tan \beta - \tan \alpha }}.\]
Substitute the known values and calculate the height \(H:\)
\[H = \frac{{L\tan \alpha \tan \beta }}{{\tan \beta - \tan \alpha }} = \frac{{187 \cdot \tan {{45}^\circ}\tan {{60}^\circ}}}{{\tan {{60}^\circ} - \tan {{45}^\circ}}} = \frac{{187 \times 1 \times \sqrt 3 }}{{\sqrt 3 - 1}} = 187 \times 2.366 = 442\,m.\]
Example 8.
Find the area of a regular \(n\text{-sided}\) polygon if the length of one side is \(a.\)
Solution.
A \(n\text{-sided}\) polygon can be split up into \(n\) triangles.
Figure 8. Each triangle has the central angle \(\frac{{{{360}^0}}}{n} = \frac{{2\pi }}{n}.\) We denote half of the central angle by \(\alpha,\) so
\[\alpha = \frac{\pi }{n}.\]
Find the apothem \(h:\)
\[h = \frac{a}{2}\cot \alpha = \frac{a}{2}\cot \frac{\pi }{n}.\]
The area of one triangle is
\[{A_0} = \frac{1}{2}ah = \frac{1}{2} \times a \times \frac{a}{2}\cot \frac{\pi }{n} = \frac{{{a^2}}}{4}\cot \frac{\pi }{n}.\]
Then the total area of an \(n\text{-sided}\) regular polygon is given by
\[A = n{A_0} = \frac{{n{a^2}}}{4}\cot \frac{\pi }{n}.\]