Radioactive Decay

In nature, there are a large number of atomic nuclei that can spontaneously emit elementary particles or nuclear fragments. Such a phenomenon is called radioactive decay. This effect was studied at the turn of 19−20 centuries by Antoine Becquerel, Marie and Pierre Curie, Frederick Soddy, Ernest Rutherford, and other scientists. As a result of the experiments, F.Soddy and E.Rutherford derived the radioactive decay law, which is given by the differential equation:

where $$ is the amount of a radioactive material, $$ is a positive constant depending on the radioactive substance. The minus sign in the right side means that the amount of the radioactive material $$ decreases over time (Figure $$).

The given equation is easy to solve, and the solution has the form:

To determine the constant $$ it is necessary to indicate an initial value. If the amount of the material at the moment $$ was $$ then the radioactive decay law is written as

Further, we introduce two useful parameters that follow from the given law.

The half life or half life period $$ of a radioactive material is the time reguired to decay to one-half of the initial value of the material. Hence, at the moment $$

The formula for the half life follows from here:

The average lifetime $$ of a radioactive atom is given by

As it can be seen, the half life $$ and the average lifetime $$ are related to each other by the formula:

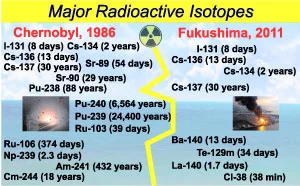
These $$ parameters vary widely for different substances. For example, the half life of Polonium-$$ is less than $$ microseconds, but the half life of Thorium-$$ is more than 1 billion years. A wide range of isotopes with different half lives was thrown from the atomic reactors and cooling pools in Chernobyl and Fukushima disasters (Figure $$).

Solved Problems

Solution.

The mass of a radioactive material decreases as a result of decay twice after each half life. So, after $$ half lives the quantity of the material will be $$ of the initial amount. Hence, the mass after decay is $$

Solution.

According to the radioactive decay law the mass of an isotope depends on time as follows:

Here the decay constant $$ is equal to

Calculate the mass of the Iodine isotope in $$ days: