Newton’s Second Law of Motion

Solved Problems

Solution.

There are two forces acting on the body (Figure $$): the force of gravity $$ and the drag force $$

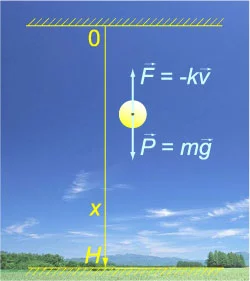
We direct the $$-axis vertically downwards. We assume that the initial coordinate is $$ and it is equal to $$ when the body hits the ground.

Considering the projection on the $$-axis the dynamics equation can be written as

This problem is a variation of Case $$ when the force depends on the velocity.

First we find the velocity $$ from the equation

Separating the variables, we have

Here, $$ is the velocity at time $$ $$ is the variable of integration. The solution is as follows:

We integrate again:

Assume that the body reaches the Earth's surface at $$ when it traverses the distance $$ As it can be seen, the time $$ is given by the implicit algebraic equation

The value of $$ can be estimated approximately, given that the term $$ approaches zero for large $$ Then

The resulting approximate dependence of $$ is linear, which corresponds to the uniform motion of the body. Its curve (for $$ $$) is shown in Figure $$ (the red line $$). For comparison, the graph shows two other curves $$ describing:

• freely falling body in the gravitational field without air resistance (the blue curve $$). In this case, the dependence $$ is defined by the formula $$
• exact solution of the nonlinear algebraic equation for $$ (the green curve $$).

It is seen from these graphs that the air resistance force compensates the force of gravity in a few seconds after the start of the drop. After that, the motion of the body becomes uniform. Therefore, when falling from a large height (in this example, more than $$), one can use the approximate formula for $$ to estimate the falling time.

Solution.

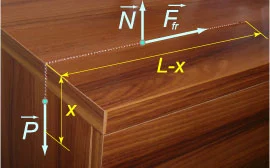
The movement of the chain is completely determined by two variable forces:

• the force of gravity $$ where $$ is the length of the chain hanging off the table, $$ is the mass of the chain, $$ is its length, $$is the standard gravity;
• the friction force $$ $$ where $$ is the coefficient of friction. The friction force acts only on the part of the chain lying on the table. The length of this part is equal to $$

According to Newton's second law, the differential equation of motion of the chain has the form:

We got a second order nonhomogeneous differential equation with constant coefficients. Let us solve this equation. First we consider the associated homogeneous equation:

The roots of the characteristic equation have the following values:

Then the general solution of the homogeneous equation can be written as

We define the constants $$ later using the initial conditions.

We now construct a particular solution of the nonhomogeneous equation. The right side is a constant expression, so we seek a particular solution in the form of a constant number: $$ Substituting $$ $$ in the original equation, we obtain:

Thus, the general solution of the inhomogeneous equation has the form:

Consider the initial conditions and determine the coefficients $$ and $$ As the chain was in equilibrium, the following equation is valid:

It follows that the length of the hanging part of the chain at equilibrium is

By the condition of the problem, at the initial time the chain gets an additional shift $$ so that the initial conditions are written as

Now we can calculate the coefficients $$ and $$

Hence, the sliding of the chain is described by

The chain slips off the table at time $$ where $$ As a result, we have the following algebraic equation for $$

The expression for $$ can be written explicitly. To do this, we multiply the equation by $$

Denoting $$ we obtain the quadratic equation:

Here we only take the root with $$ sign to satisfy the inequality

Hence, the solution is given by

Interestingly, the time of sliding $$ in this model depends essentially on the initial displacement $$ with respect to the equilibrium position. As $$ we formally get $$ Dependence of the time of sliding $$ on the displacement $$ for chains of different lengths $$ is shown above in Figure $$