Floor and Ceiling Functions
Solved Problems
Example 1.
Solve the equation
\(\left\lfloor {x - \frac{1}{2}} \right\rfloor + \left\lfloor {x - \frac{5}{2}} \right\rfloor\) \(+\, \left\lfloor {x - \frac{9}{2}} \right\rfloor = 3.\)
Solution.
Change the variable: \(x - \frac{1}{2} = z.\) Then the equation becomes
\[\left\lfloor z \right\rfloor + \left\lfloor {z - 2} \right\rfloor + \left\lfloor {z - 4} \right\rfloor = 3.\]
Using the identity \(\left\lfloor {x + n} \right\rfloor = \left\lfloor x \right\rfloor + n,\) we get
\[\left\lfloor z \right\rfloor + \left\lfloor z \right\rfloor - 2 + \left\lfloor z \right\rfloor - 4 = 3,\;\; \Rightarrow 3\left\lfloor z \right\rfloor = 9,\;\; \Rightarrow \left\lfloor z \right\rfloor = 3.\]
The last equation means that \(3 \le z \lt 4.\) Returning back to the variable \(x,\) we have
\[3 \le x - \frac{1}{2} \lt 4,\;\; \Rightarrow 3\frac{1}{2} \le x \lt 4\frac{1}{2},\;\text{ or }\;x \in \left[ {3.5,4.5} \right).\]
Example 2.
Solve the equation \({x^2} + 2{\left\{ x \right\}^2} = 12.\)
Solution.
Since, by definition, \(0 \le \left\{ x \right\} \lt 1,\) then
\[0 \le {\left\{ x \right\}^2} \lt 1,\;\; \Rightarrow 0 \le 2{\left\{ x \right\}^2} \lt 2.\]
Hence,
\[10 \lt {x^2} \le 12.\]
Given that \(x^2\) is an increasing function for \(x \gt 0,\) we get
\[\sqrt {10} \lt x \le \sqrt {12} ,\]
that is, the floor of \(x\) is equal to \(3.\) Hence, we can represent the number \(x\) as
\[x = \left\lfloor x \right\rfloor + \left\{ x \right\} = 3 + \theta ,\]
where \(\theta\) is the fractional part of \(x.\)
Substitute this expression into the original equation and solve it for \(\theta.\)
\[{\left( {3 + \theta } \right)^2} + 2{\theta ^2} = 12,\;\; \Rightarrow 9 + 6\theta + {\theta ^2} + 2{\theta ^2} = 12,\;\; \Rightarrow 3{\theta ^2} + 6\theta = 3,\;\; \Rightarrow {\theta ^2} + 2\theta = 1,\;\; \Rightarrow {\theta ^2} + 2\theta + 1 = 2,\;\; \Rightarrow {\left( {\theta + 1} \right)^2} = 2,\;\; \Rightarrow \theta + 1 = \sqrt 2 ,\;\; \Rightarrow \theta = \sqrt 2 - 1.\]
Therefore,
\[x = 3 + \theta = 3 + \sqrt 2 - 1 = 2 + \sqrt 2 .\]
Example 3.
Find all \(x\) satisfying the equation \(\left\{ {3x} \right\} = \frac{1}{3}.\)
Solution.
Since \(3x = \left\lfloor {3x} \right\rfloor + \left\{ {3x} \right\},\) we rewrite the equation in the form
\[\left\{ {3x} \right\} = \frac{1}{3},\;\; \Rightarrow 3x - \left\lfloor {3x} \right\rfloor = \frac{1}{3},\;\; \Rightarrow \left\lfloor {3x} \right\rfloor = 3x - \frac{1}{3}.\]
The \(RHS\) must be an integer. We denote it by \(n,\) so
\[3x - \frac{1}{3} = n,\;\; \Rightarrow 3x = n + \frac{1}{3},\;\; \Rightarrow x = \frac{n}{3} + \frac{1}{9},\; n \in \mathbb{Z}.\]
Then we have
\[\left\lfloor {3x} \right\rfloor = 3x - \frac{1}{3},\;\; \Rightarrow \left\lfloor {3\left( {\frac{n}{3} + \frac{1}{9}} \right)} \right\rfloor = n,\;\; \Rightarrow \left\lfloor {n + \frac{1}{3}} \right\rfloor = n.\]
It follows from the last equation that
\[n \le n + \frac{1}{3} \lt n + 1.\]
This double inequality is valid for any \(n \in \mathbb{Z}.\) Hence, the solution set is given by
\[x = \left\{ {n \in \mathbb{Z} \,\bigg|\, \frac{n}{3} + \frac{1}{9}} \right\}.\]
We can check the answer for a few values of \(n:\)
\(n = -1:\)
\[x = - \frac{2}{9},\;\; \Rightarrow \left\{ {3x} \right\} = \left\{ {3 \cdot \left( { - \frac{2}{9}} \right)} \right\} = \left\{ { - \frac{2}{3}} \right\} = \left\{ { - 1 + \frac{1}{3}} \right\} = \frac{1}{3};\]
\(n = 0:\)
\[x = \frac{1}{9},\;\; \Rightarrow \left\{ {3x} \right\} = \left\{ {\frac{1}{3}} \right\} = \frac{1}{3};\]
\(n = 2:\)
\[x = \frac{7}{9},\;\; \Rightarrow \left\{ {3x} \right\} = \left\{ {3 \cdot \frac{7}{9}} \right\} = \left\{ {\frac{7}{3}} \right\} = \left\{ {2 + \frac{1}{3}} \right\} = \frac{1}{3}.\]
Example 4.
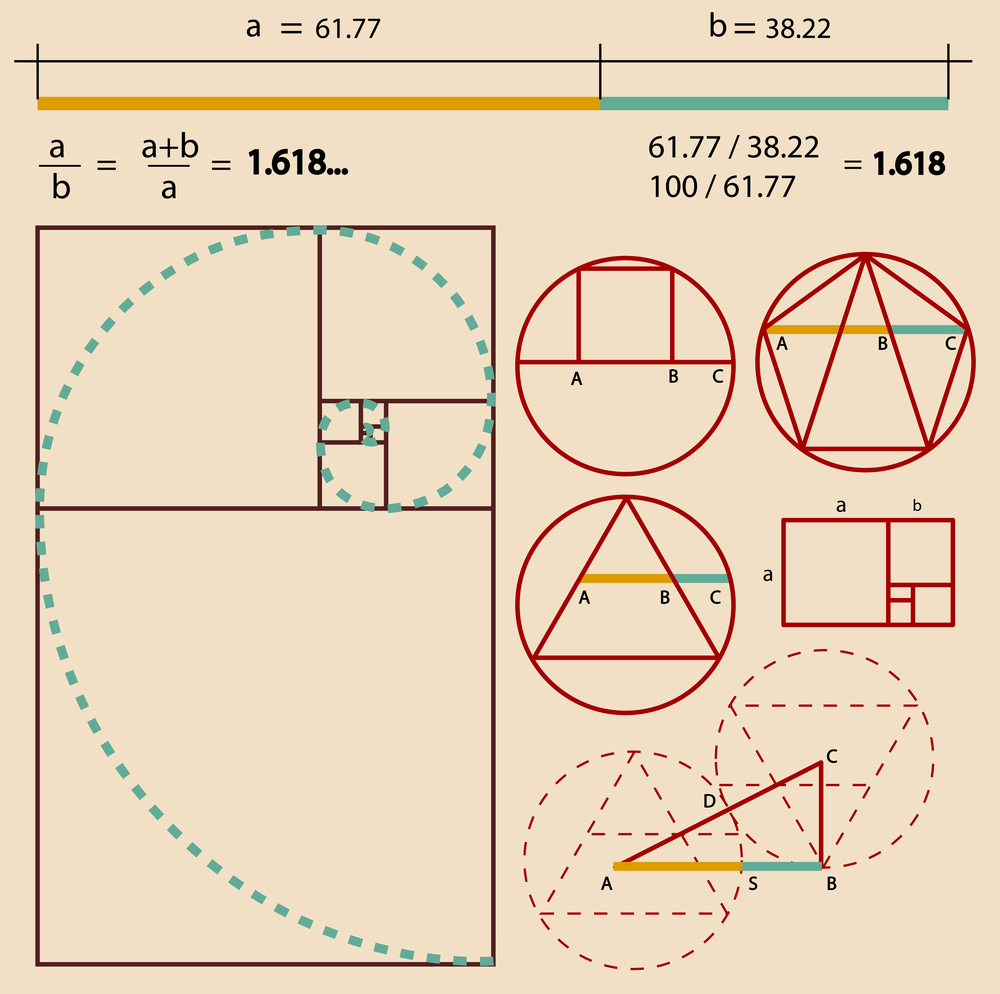
Prove that \(\left\{ \varphi \right\} =\frac{1}{\varphi },\) where \(\varphi = \frac{{1+\sqrt 5}}{2}\) is the golden ratio .
Solution.
We represent the golden ratio \(\varphi\) as
\[\varphi = \frac{{1 + \sqrt 5 }}{2} = \frac{{1 + \sqrt 5 + 1 - 1}}{2} = \frac{{2 + \sqrt 5 - 1}}{2} = 1 + \frac{{\sqrt 5 - 1}}{2} = \left\lfloor \varphi \right\rfloor + \left\{ \varphi \right\},\]
so the fractional part of \(\varphi\) is given by
\[\left\{ \varphi \right\} = \frac{{\sqrt 5 - 1}}{2} \approx 0.618\ldots\]
Figure 4. Calculate the reciprocal \(\frac{1}{\varphi } :\)
\[\frac{1}{\varphi } = \frac{1}{{\frac{{1 + \sqrt 5 }}{2}}} = \frac{2}{{1 + \sqrt 5 }} = \frac{{2\left( {1 - \sqrt 5 } \right)}}{{\left( {1 + \sqrt 5 } \right)\left( {1 - \sqrt 5 } \right)}} = \frac{{2\left( {1 - \sqrt 5 } \right)}}{{{1^2} - {{\left( {\sqrt 5 } \right)}^2}}} = \frac{{2\left( {1 - \sqrt 5 } \right)}}{{1 - 5}} = \frac{{2\left( {\sqrt 5 - 1} \right)}}{4} = \frac{{\sqrt 5 - 1}}{2}.\]
Hence,
\[\left\{ \varphi \right\} = \frac{1}{\varphi }.\]
Example 5.
Solve the equation \({x^3} - \left\lfloor x \right\rfloor = 5.\)
Solution.
We represent the number \(x\) as
\[x = \left\lfloor x \right\rfloor + \left\{ x \right\},\]
where the fractional part \(\left\{ x \right\}\) satisfies the condition \(0 \le \left\{ x \right\} \lt 1.\)
Substitute \(\left\lfloor x \right\rfloor = x - \left\{ x \right\}\) in the equation to get
\[{x^3} - \left\lfloor x \right\rfloor = 5,\;\; \Rightarrow {x^3} - \left( {x - \left\{ x \right\}} \right) = 5,\;\; \Rightarrow {x^3} - x + \left\{ x \right\} = 5,\;\; \Rightarrow \left\{ x \right\} = x - {x^3} + 5.\]
It is clear that
\[0 \le x - {x^3} + 5 \lt 1,\;\; \Rightarrow - 5 \le x - {x^3} \lt - 4,\;\; \Rightarrow 4 \lt {x^3} - x \le 5.\]
By taking the derivative of the function \(f\left( x \right) = {x^3} - x\) we find its local extrema :
\[f^{\prime}\left( x \right) = \left( {{x^3} - x} \right)^{\prime} = 3{x^2} - 1 = 0,\;\; \Rightarrow {x_{1,2}} = \pm \frac{1}{{\sqrt 3 }}.\]
The function \(f\left( x \right)\) is increasing on the intervals \(\left( { - \infty , - \frac{1}{{\sqrt 3 }}} \right)\) and \(\left( {\frac{1}{{\sqrt 3 }},\infty } \right),\) and is decreasing on the interval \(\left( { - \frac{1}{{\sqrt 3 }},\frac{1}{{\sqrt 3 }}} \right).\) The maximum value on the interval \(\left( { - \infty ,\frac{1}{{\sqrt 3 }}} \right)\) is attained at \({{x_1} = - \frac{1}{{\sqrt 3 }}}:\)
\[f\left( {{x_1}} \right) = f\left( { - \frac{1}{{\sqrt 3 }}} \right) = {\left( { - \frac{1}{{\sqrt 3 }}} \right)^3} - \left( { - \frac{1}{{\sqrt 3 }}} \right) = - \frac{1}{{3\sqrt 3 }} + \frac{1}{{\sqrt 3 }} = \frac{2}{{3\sqrt 3 }} \lt 4.\]
Thus, the function takes the values from \(4\) to \(5\) on the last interval \(\left( {\frac{1}{{\sqrt 3 }},\infty } \right)\) where it is strictly increasing . Note that
\[f\left( 1 \right) = {1^3} - 1 = 0,\;\;f\left( 2 \right) = {2^3} - 2 = 6.\]
So, the solution of the equation must be in the range \(1 \lt x \lt 2,\) that is, \(\left\lfloor x \right\rfloor = 1.\) This yields:
\[{x^3} - \left\lfloor x \right\rfloor = 5,\;\; \Rightarrow {x^3} - 1 = 5,\;\; \Rightarrow {x^3} = 6,\;\; \Rightarrow x = \sqrt[3]{6}.\]
Example 6.
Solve the equation \({x^2} = \left\lfloor x \right\rfloor + 1.\)
Solution.
We rewrite the equation in the form
\[\left\lfloor x \right\rfloor = {x^2} - 1.\]
Note that \(x^2 -1 \ge -1\) in the right hand side. Hence, \(x \ge -1\) in the left hand side, too. From these conditions, we have
\[\left\{ \begin{array}{l} {x^2} - 1 \ge -1\\ x \ge -1 \end{array} \right.,\;\; \Rightarrow \left\{ \begin{array}{l} {x^2} \ge 0\\ x \ge -1 \end{array} \right.,\;\; \Rightarrow x \ge -1.\]
The original equation is equivalent to the following system:
\[\left\{ \begin{array}{l} {x^2} - 1 = n\\ n \le x \lt n + 1 \end{array} \right.,\]
where \(n \ge -1\) is an integer.
Express \(x\) in terms of \(n\) from the first equation:
\[{x^2} = n + 1,\;\; \Rightarrow x = \sqrt {n + 1} ,\]
and substitute \(x\) in the second expression:
\[n \le x \lt n + 1,\;\; \Rightarrow n \le \sqrt {n + 1} \lt n + 1,\;\; \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{n \le \sqrt {n + 1} }\\
{\sqrt {n + 1} \lt n + 1}
\end{array}} \right..\]
The first inequality in the system has the following solution:
\[n \le \sqrt {n + 1} ,\;\; \Rightarrow {n^2} \le n + 1,\;\; \Rightarrow {n^2} - n \le 1,\;\; \Rightarrow {n^2} - n + \frac{1}{4} \le \frac{5}{4},\;\; \Rightarrow {\left( {n - \frac{1}{2}} \right)^2} \le \frac{5}{4},\;\; \Rightarrow - \frac{{\sqrt 5 }}{2} \le n - \frac{1}{2} \le \frac{{\sqrt 5 }}{2},\;\; \Rightarrow \frac{{1 - \sqrt 5 }}{2} \le n \le \frac{{1 + \sqrt 5 }}{2},\]
or approximately \( - 0.61 \lt n \lt 1.62.\) Since \(n \ge -1,\) there are only \(2\) values satisfying the first inequality: \(n = 0, 1.\)
Consider the second inequality:
\[\sqrt {n + 1} \lt n + 1,\;\; \Rightarrow n + 1 \lt {\left( {n + 1} \right)^2},\;\; \Rightarrow n + 1 \lt {n^2} + 2n + 1,\;\; \Rightarrow {n^2} + n \gt 0,\;\; \Rightarrow n\left( {n + 1} \right) \gt 0,\;\; \Rightarrow n \in \left( { - \infty , - 1} \right) \cup \left( {0,\infty } \right).\]
The common solution of the two inequalities is \(n = 1.\) Therefore,
\[x = \sqrt {n + 1} = \sqrt 2 .\]