Derivatives of Polar Functions
Solved Problems
Example 7.
Find the angle \(\alpha\) between the polar curves \({r_1} = {e^\theta }\) and \({r_2} = {e^{-\theta}}\) at the point of intersection.
Solution.
We first determine the coordinates of the point of intersection of these curves:
\[{r_1} = {r_2},\;\; \Rightarrow {e^\theta } = {e^{ - \theta }},\;\; \Rightarrow \theta = - \theta ,\;\; \Rightarrow \theta = 0.\]
So the curves intersect at \(\theta = 0.\)
Compute the derivative of each curve by the formula
\[\frac{{dy}}{{dx}} = \frac{{f^\prime\left( \theta \right)\sin \theta + f\left( \theta \right)\cos \theta }}{{f^\prime\left( \theta \right)\cos \theta - f\left( \theta \right)\sin \theta }}.\]
For the \(1\)st curve \({r_1} = {e^\theta }:\)
\[\require{cancel} \frac{{dy}}{{dx}} = \frac{{\left( {{e^\theta }} \right)^\prime\sin \theta + {e^\theta }\cos \theta }}{{\left( {{e^\theta }} \right)^\prime\cos \theta - {e^\theta }\sin \theta }} = \frac{{{e^\theta }\sin \theta + {e^\theta }\cos \theta }}{{{e^\theta }\cos \theta - {e^\theta }\sin \theta }} = \frac{{\cancel{e^\theta }\left( {\sin \theta + \cos \theta } \right)}}{{\cancel{e^\theta }\left( {\cos \theta - \sin \theta } \right)}} = \frac{{\sin \theta + \cos \theta }}{{\cos \theta - \sin \theta }}.\]
So for \(\theta = 0\) we have
\[\frac{{dy}}{{dx}}{\left( {\theta = 0} \right)_1} = \frac{{\sin 0 + \cos 0}}{{\cos 0 - \sin 0}} = \frac{{0 + 1}}{{1 - 0}} = 1.\]
Similarly we calculate the derivative for the \(2\)nd curve \({r_2} = {e^{-\theta}}:\)
\[\frac{{dy}}{{dx}} = \frac{{\left( {{e^{ - \theta }}} \right)'\sin \theta + {e^{ - \theta }}\cos \theta }}{{\left( {{e^{ - \theta }}} \right)'\cos \theta - {e^{ - \theta }}\sin \theta }} = \frac{{ - {e^{ - \theta }}\sin \theta + {e^{ - \theta }}\cos \theta }}{{ - {e^{ - \theta }}\cos \theta - {e^{ - \theta }}\sin \theta }} = \frac{{\cancel{e^{ - \theta }}\left( {\cos \theta - \sin \theta } \right)}}{{\cancel{e^{ - \theta }}\left( { - \cos \theta - \sin \theta } \right)}} = \frac{{\sin \theta - \cos \theta }}{{\sin \theta + \cos \theta }}.\]
Then
\[\frac{{dy}}{{dx}}{\left( {\theta = 0} \right)_2} = \frac{{\sin 0 - \cos 0}}{{\sin 0 + \cos 0}}= \frac{{0 - 1}}{{0 + 1}} = - 1.\]
The angle between two curves is equal to the angle between the corresponding tangent lines to the curves at the point of tangency. As the slopes of the tangents are \({k_1} = 1\) and \({k_2} = -1,\) the angle \(\alpha\) between the curves is given by
\[\tan \alpha = \frac{{{k_1} - {k_2}}}{{1 + {k_1}{k_2}}} = \frac{{ - 1 - 1}}{{1 + 1 \cdot \left( { - 1} \right)}} = \infty .\]
This means that \(\alpha = \frac{\pi }{2}.\)
Example 8.
Find the derivative \(\frac{{dy}}{{dx}}\) of the hyperbolic spiral \(r = \frac{a}{\theta }.\)
Solution.
We compute the derivative \(\frac{{dy}}{{dx}}\) by the formula
\[\frac{{dy}}{{dx}} = \frac{{f^\prime\left( \theta \right)\sin \theta + f\left( \theta \right)\cos \theta }}{{f^\prime\left( \theta \right)\cos \theta - f\left( \theta \right)\sin \theta }}.\]
Since \(r = \frac{a}{\theta },\) we obtain
\[f^\prime\left( \theta \right) = \left( {\frac{a}{\theta }} \right)^\prime = - \frac{a}{{{\theta ^2}}}.\]
The derivative is given by
\[\frac{{dy}}{{dx}} = \frac{{\left( { - \frac{a}{{{\theta ^2}}}} \right)\sin \theta + \frac{a}{\theta }\cos \theta }}{{\left( { - \frac{a}{{{\theta ^2}}}} \right)\cos \theta - \frac{a}{\theta }\sin \theta }} = \frac{{ - \sin \theta + \theta \cos \theta }}{{ - \cos \theta - \theta \sin \theta }} = \frac{{\sin \theta - \theta \cos \theta }}{{\cos \theta + \theta \sin \theta }} = \frac{{\tan \theta - \theta }}{{1 + \theta \tan \theta }} = \frac{{\tan \theta - \tan \left( {\arctan \theta } \right)}}{{1 + \tan \left( {\arctan \theta } \right) \cdot \tan \theta }}.\]
Using the tangent subtraction identity
\[\tan \left( {\alpha - \beta } \right) = \frac{{\tan \alpha - \tan \beta }}{{1 + \tan \alpha \tan \beta }},\]
we get
\[\frac{{dy}}{{dx}} = \tan \left( {\theta - \arctan \theta } \right).\]
Example 9.
Find the derivative \(\frac{{dy}}{{dx}}\) of the circle and calculate its values for the polar angles \(\theta = {\frac{\pi }{4}},{\frac{{3\pi }}{4}}.\)
Solution.
The equation of a circle in polar coordinates has a very simple form:
\[r = f\left( \theta \right) = R,\]
where \(R\) is the radius of the circle.
Hence, given that \(f'\left( \theta \right) = 0\), we can easily find the derivative \(\frac{{dy}}{{dx}}\) of the circle:
\[\frac{{dy}}{{dx}} = {y'_x} = \frac{{{y'_\theta }}}{{{x'_\theta }}} = \frac{{f'\left( \theta \right)\sin \theta + f\left( \theta \right)\cos\theta }}{{f'\left( \theta \right)\cos\theta - f\left( \theta \right)\sin\theta }} = \frac{{0 \cdot \sin \theta + R\cos\theta }}{{0 \cdot \cos\theta - R\sin\theta }} = - \cot \theta .\]
In particular, for the angles \(\frac{\pi }{4}\) and \(\frac{3\pi }{4}\), the derivative is equal:
\[{\frac{{dy}}{{dx}}\left( {\theta = \frac{\pi }{4}} \right) = - \cot\frac{\pi }{4} = - 1,\;\;}{\frac{{dy}}{{dx}}\left( {\theta = \frac{{3\pi }}{4}} \right) = - \cot\frac{{3\pi }}{4} = 1.}\]
As it is known, the value of the derivative at a point is equal to the slope of the tangent line drawn to the curve at this point. For the specified angles, this is illustrated schematically in Figure \(8.\)
Figure 8.
Example 10.
Find the derivative \(\frac{{dy}}{{dx}}\) of the lemniscate of Bernoulli given by the equation
\[{r^2} = \cos 2\theta .\]
Solution.
We will consider this curve in the range of angles at which
\[\cos 2\theta \gt 0.\]
Solving this inequality, we obtain:
\[\cos 2\theta \gt 0,\;\; \Rightarrow - \frac{\pi }{2} + 2\pi n \lt 2\theta \lt \frac{\pi }{2} + 2\pi n, \Rightarrow - \frac{\pi }{4} + \pi n \lt \theta \lt \frac{\pi }{4} + \pi n,\;\;n \in \mathbb{Z}.\]
We choose a bounded interval \( - {\frac{\pi }{4}} \lt \theta \lt {\frac{\pi }{4}},\) corresponding to one lobe of the Bernoulli's lemniscate (see Figure \(9\) below). In this interval, the equation of the curve can be written as
\[r = f\left( \theta \right) = \sqrt {\cos 2\theta } .\]
The derivative of this function is
\[f'\left( \theta \right) = {\left( {\sqrt {\cos 2\theta } } \right)^\prime } = \frac{1}{{2\sqrt {\cos 2\theta } }} \cdot {\left( {\cos 2\theta } \right)^\prime } = \frac{1}{{2\sqrt {\cos 2\theta } }} \cdot \left( { - \sin 2\theta } \right) \cdot 2 = - \frac{{\sin 2\theta }}{{\sqrt {\cos 2\theta } }}.\]
Then the derivative \(\frac{{dy}}{{dx}}\) is described by the following expression:
\[\frac{{dy}}{{dx}} = {y'_x} = \frac{{{y'_\theta }}}{{{x'_\theta }}} = \frac{{f'\left( \theta \right)\sin \theta + f\left( \theta \right)\cos\theta }}{{f'\left( \theta \right)\cos\theta - f\left( \theta \right)\sin\theta }} = \frac{{\left( { - \frac{{\sin 2\theta }}{{\sqrt {\cos 2\theta } }}} \right)\sin \theta + \sqrt {\cos 2\theta } \cos\theta }}{{\left( { - \frac{{\sin 2\theta }}{{\sqrt {\cos 2\theta } }}} \right)\cos\theta - \sqrt {\cos 2\theta } \sin\theta }} = - \frac{{\frac{{\cos 2\theta \cos \theta - \sin 2\theta \sin \theta }}{{\cancel{\sqrt {\cos 2\theta }} }}}}{{\frac{{\sin 2\theta \cos \theta + \cos 2\theta \sin \theta }}{{\cancel{\sqrt {\cos 2\theta }} }}}} = - \frac{{\cos 2\theta \cos \theta - \sin 2\theta \sin \theta }}{{\sin 2\theta \cos \theta + \cos 2\theta \sin \theta }}.\]
The numerator and denominator can be simplified using the trigonometric identities
\[{\cos\left( {\alpha + \beta } \right) = \cos \alpha \cos \beta - \sin \alpha \sin \beta ,\;\;}{\sin \left( {\alpha + \beta } \right) = \sin \alpha \cos \beta + \cos \alpha \sin \beta.}\]
Hence,
\[\frac{{dy}}{{dx}} = - \frac{{\cos 2\theta \cos \theta - \sin 2\theta \sin \theta }}{{\sin 2\theta \cos \theta + \cos 2\theta \sin \theta }} = - \frac{{\cos \left( {2\theta + \theta } \right)}}{{\sin \left( {2\theta + \theta } \right)}} = - \frac{{\cos 3\theta }}{{\sin 3\theta }} = - \cot 3\theta .\]
Note that the function \(\cot 3\theta \) is not defined at the point where
\[3\theta = \pi n,\;\; \Rightarrow \theta = \frac{{\pi n}}{3},\;\;n \in \mathbb{Z}\;\; \Rightarrow \theta = 0, \pm \frac{\pi }{3}, \pm \frac{{2\pi }}{3}, \ldots\]
Only one point \(\theta = 0\) falls in our interval \(\left( { - {\frac{\pi }{4}},{\frac{\pi }{4}}} \right).\) The derivative at this point has an infinite discontinuity. The tangent to the curve at this point is a vertical line \(\left({\text{Figure }9}\right).\)
Figure 9. Lemniscate of Bernoulli
Example 11.
Find the derivative \(\frac{{dy}}{{dx}}\) of Galileo's spiral .
Solution.
Galileo's spiral describes the trajectory of a freely falling body in a coordinate system involving rotation of the Earth. We derive the equation of the curve in polar coordinates.
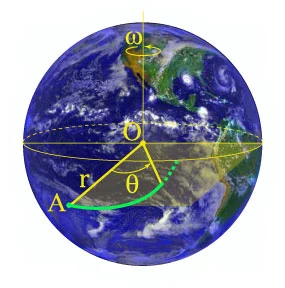
Suppose a body begins to fall from a point \(A\) directly above the Earth's equator (Fig.\(10\)) The motion along the radius-vector \(r\) is uniformly accelerated and is given by
\[r = H + R - \frac{{g{t^2}}}{2},\]
where \(H\) is the initial height of the body above the Earth, \(R\) is the radius of the Earth, \(g\) is the acceleration of gravity, \(t\) is time.
Figure 10. Trajectory of a Falling Body Simultaneously with the falling of the body, the Earth rotates with a constant angular velocity \(\omega\). In this case, the rotation angle \(\theta\) varies in time as
\[\theta = \omega t = \frac{{2\pi }}{T}t,\]
where \(\omega\) is the angular velocity of rotation of the Earth, \(T\) is the period of rotation \(\left({T = 24\;\text{hours} = 86,400\;\text{sec}}\right).\)
Thus, the parametric equations of the curve have the form:
\[\left\{ \begin{array}{l} r = H + R - \frac{{g{t^2}}}{2}\\ \theta = \frac{{2\pi }}{T}t \end{array} \right..\]
Eliminating the parameter \(t,\) we obtain the polar equation of the trajectory:
\[t = \frac{T}{{2\pi }}\theta ,\;\; \Rightarrow r = H + R - \frac{g}{2}{\left( {\frac{T}{{2\pi }}\theta } \right)^2} = H + R - \frac{{g{T^2}}}{{8{\pi ^2}}}{\theta ^2}.\]
This equation is convenient to write in the form
\[r\left( \theta \right) = a{\theta ^2} - d,\;\;\text{where}\;\;a = - \frac{{g{T^2}}}{{8{\pi ^2}}},\;\;d = - \left( {H + R} \right).\]
The given equation is called the polar equation of Galileo's spiral . In our model, one turn of the spiral corresponds to one revolution of the Earth. It is clear that for real fall time values, the trajectory of a body is described by a rather short portion of the spiral.
Focusing on the variable (quadratic) term \(a{\theta ^2}\), we consider the case \(d = 0.\) Then the equation of the spiral takes the following form:
\[r = f\left( \theta \right) = a{\theta ^2}.\]
As seen in Figure \(11\), the Galileo's spiral is similar to the Archimedean spiral, but differs from it in that the length of the radius vector increases much faster, in accordance with the square law. The distance between successive turnings of Galileo's spiral also increases by the same law.
Figure 11. Galileo’s Spiral Find the derivative of the above polar function:
\[r'\left( \theta \right) = f'\left( \theta \right) = {\left( {a{\theta ^2}} \right)^\prime } = 2a\theta .\]
Substituting this into the formula for \(\frac{{dy}}{{dx}}\), we obtain
\[\frac{{dy}}{{dx}} = {y'_x} = \frac{{{y'_\theta }}}{{{x'_\theta }}} = \frac{{f'\left( \theta \right)\sin \theta + f\left( \theta \right)\cos\theta }}{{f'\left( \theta \right)\cos\theta - f\left( \theta \right)\sin\theta }} = \frac{{2a\theta \sin \theta + a{\theta ^2}\cos\theta }}{{2a\theta \cos\theta - a{\theta ^2}\sin\theta }} = \frac{{\cancel{a\theta} \left( {2\sin \theta + \theta \cos\theta } \right)}}{{\cancel{a\theta} \left( {2\cos\theta - \theta \sin\theta } \right)}} = \frac{{2\tan\theta + \theta }}{{2 - \theta \tan \theta }} = \frac{{2\tan\theta + 2 \cdot \frac{\theta }{2}}}{{2 - 2 \cdot \frac{\theta }{2} \cdot \tan \theta }} = \frac{{\cancel{2}\left( {\tan\theta + \frac{\theta }{2}} \right)}}{{\cancel{2}\left( {1 - \tan \theta \cdot \frac{\theta }{2}} \right)}} = \frac{{\tan\theta + \frac{\theta }{2}}}{{1 - \tan \theta \cdot \frac{\theta }{2}}}.\]
Again, as in problem \(1\), represent the angle \({\frac{\theta }{2}}\) in the form
\[\frac{\theta }{2} = \tan \left( {\arctan \frac{\theta }{2}} \right)\]
and apply the tangent addition formula :
\[\tan \left( {\alpha + \beta } \right) = \frac{{\tan \alpha + \tan \beta }}{{1 - \tan \alpha \cdot \tan \beta }}.\]
As a result, we find the final expresion for the derivative \(\frac{{dy}}{{dx}}\) of Galileo's spiral:
\[\frac{{dy}}{{dx}} = \frac{{\tan \theta + \frac{\theta }{2}}}{{1 - \tan \theta \cdot \frac{\theta }{2}}} = \frac{{\tan \theta + \tan \left( {\arctan \frac{\theta }{2}} \right)}}{{1 - \tan \theta \cdot \tan \left( {\arctan \frac{\theta }{2}} \right)}} = \tan \left( {\theta + \arctan \frac{\theta }{2}} \right).\]
Example 12.
Find the derivative \(\frac{{dy}}{{dx}}\) of Fermat's spiral given by the polar equation
\[r = \sqrt \theta.\]
Solution.
In Fermat's spiral, the radius \(r\) increases by the square root law with increasing the angle \(\theta\), i.e. rather slowly. The density of turns also increases with the growth of \(r\), as shown in Figure \(12.\)
Figure 12. Fermat’s Spiral (2 Branches) This type of spirals is also found in nature. For example, the seeds in sunflowers are arranged along the curves resembling a Fermat's spiral (Figure \(13\)).
Figure 13. Sunflower Spirals Returning to the subject of the problem, we calculate the derivative \(\frac{{dy}}{{dx}}\) of the given curve.
First we find the derivative \(f'\left( \theta \right)\) in polar coordinates:
\[r'\left( \theta \right) = f'\left( \theta \right) = \frac{1}{{2\sqrt \theta }}.\]
Consequently, the derivative in Cartesian coordinates is expressed by the following formula:
\[\frac{{dy}}{{dx}} = {y'_x} = \frac{{{y'_\theta }}}{{{x'_\theta }}} = \frac{{f'\left( \theta \right)\sin \theta + f\left( \theta \right)\cos \theta }}{{f'\left( \theta \right)\cos\theta - f\left( \theta \right)\sin\theta }} = \frac{{\frac{1}{{2\sqrt \theta }}\sin \theta + \sqrt \theta \cos \theta }}{{\frac{1}{{2\sqrt \theta }}\cos\theta - \sqrt \theta \sin\theta }} = \frac{{\frac{{\sin \theta + 2\theta \cos \theta }}{{\cancel{2\sqrt \theta} }}}}{{\frac{{\cos\theta - 2\theta \sin \theta }}{{\cancel{2\sqrt \theta} }}}} = \frac{{\sin \theta + 2\theta \cos \theta }}{{\cos\theta - 2\theta \sin \theta }} = \frac{{\tan \theta + 2\theta }}{{1 - 2\theta \tan \theta }}.\]
Represent here the angle \(2\theta\) as
\[2\theta = \tan\left( {\arctan 2\theta } \right)\]
and apply the tangent addition formula :
\[\tan \left( {\alpha + \beta } \right) = \frac{{\tan \alpha + \tan \beta }}{{1 - \tan \alpha \cdot \tan \beta }}.\]
Then the derivative \(\frac{{dy}}{{dx}}\) takes the following simple form:
\[\frac{{dy}}{{dx}} = \frac{{\tan \theta + 2\theta }}{{1 - 2\theta \tan \theta }} = \frac{{\tan \theta + \tan \left( {\arctan 2\theta } \right)}}{{1 - \tan \theta \cdot \tan \left( {\arctan 2\theta } \right)}} = \tan \left( {\theta + \arctan 2\theta } \right).\]
Example 13.
Find the derivative \(\frac{{dy}}{{dx}}\) of the polar curve \(r = \frac{a}{{\sqrt \theta }}\) (the lituus curve).
Solution.
We compute the derivative \(\frac{{dy}}{{dx}}\) by the formula
\[\frac{{dy}}{{dx}} = \frac{{f^\prime\left( \theta \right)\sin \theta + f\left( \theta \right)\cos \theta }}{{f^\prime\left( \theta \right)\cos \theta - f\left( \theta \right)\sin \theta }}.\]
As \(f\left( \theta \right) = \frac{a}{{\sqrt \theta }},\) we have
\[f^\prime\left( \theta \right) = \left( {\frac{a}{{\sqrt \theta }}} \right)^\prime = \left( {a{\theta ^{ - \frac{1}{2}}}} \right)^\prime = - \frac{1}{2}{\theta ^{ - \frac{3}{2}}} = - \frac{a}{{2\sqrt {{\theta ^3}} }}.\]
The derivative is given by
\[\frac{{dy}}{{dx}} = \frac{{\left( { - \frac{a}{{2\sqrt {{\theta ^3}} }}} \right)\sin \theta + \frac{a}{{\sqrt \theta }}\cos \theta }}{{\left( { - \frac{a}{{2\sqrt {{\theta ^3}} }}} \right)\cos \theta - \frac{a}{{\sqrt \theta }}\sin \theta }} = \frac{{ - a\sin \theta + 2a\theta \cos \theta }}{{ - a\cos \theta - 2a\theta \sin \theta }} = \frac{{\sin \theta - 2\theta \cos \theta }}{{\cos \theta + 2\theta \sin \theta }} = \frac{{\tan \theta - 2\theta }}{{1 + \tan \theta \cdot 2\theta }}.\]
Using the tangent subtraction formula, we can write
\[\frac{{dy}}{{dx}} = \frac{{\tan \theta - 2\theta }}{{1 + \tan \theta \cdot 2\theta }} = \frac{{\tan \theta - \tan \left( {\arctan 2\theta } \right)}}{{1 + \tan \theta \cdot \tan \left( {\arctan 2\theta } \right)}} = \tan \left( {\theta - \arctan 2\theta } \right).\]
Example 14.
Compute the derivative \(\frac{{dy}}{{dx}}\) of the polar curve \(r = {\sin ^2}\theta\) at \(\theta = \frac{\pi }{3}.\)
Solution.
The derivative \(\frac{{dy}}{{dx}}\) is given by the formula
\[\frac{{dy}}{{dx}} = \frac{{f^\prime\left( \theta \right)\sin \theta + f\left( \theta \right)\cos \theta }}{{f^\prime\left( \theta \right)\cos \theta - f\left( \theta \right)\sin \theta }}.\]
As \(f\left( \theta \right) = {\sin ^2}\theta ,\) we get
\[f^\prime\left( \theta \right) = \left( {{{\sin }^2}\theta } \right)^\prime = 2\sin \theta \cos \theta .\]
Hence
\[\frac{{dy}}{{dx}} = \frac{{2\sin \theta \cos \theta \sin \theta + {{\sin }^2}\theta \cos \theta }}{{2\sin \theta \cos \theta \cos \theta - {{\sin }^2}\theta \sin \theta }} = \frac{{3{{\sin }^2}\theta \cos \theta }}{{\sin \theta \left( {2{{\cos }^2}\theta - {{\sin }^2}\theta } \right)}} = \frac{{3\sin \theta \cos \theta }}{{2{{\cos }^2}\theta - {{\sin }^2}\theta }}.\]
Substitute \(\theta = \frac{\pi }{3} :\)
\[\frac{{dy}}{{dx}}\left( {\theta = \frac{\pi }{3}} \right) = \frac{{3\sin \frac{\pi }{3}\cos \frac{\pi }{3}}}{{2{{\cos }^2}\frac{\pi }{3} - {{\sin }^2}\frac{\pi }{3}}} = \frac{{3 \cdot \frac{{\sqrt 3 }}{2} \cdot \frac{1}{2}}}{{2 \cdot {{\left( {\frac{1}{2}} \right)}^2} - {{\left( {\frac{{\sqrt 3 }}{2}} \right)}^2}}} = \frac{{\frac{{3\sqrt 3 }}{4}}}{{ - \frac{1}{4}}} = - 3\sqrt 3 .\]
Example 15.
Find the derivative \(\frac{{dy}}{{dx}}\) of the polar function \(r = \cot \theta\) at \(\theta = \frac{\pi }{6}.\)
Solution.
The derivative \(\frac{{dy}}{{dx}}\) for a polar function \(r = f\left( \theta \right)\) is given by
\[\frac{{dy}}{{dx}} = \frac{{f^\prime\left( \theta \right)\sin \theta + f\left( \theta \right)\cos \theta }}{{f^\prime\left( \theta \right)\cos \theta - f\left( \theta \right)\sin \theta }}.\]
In our case, \(r = f\left( \theta \right) = \cot \theta .\) Then
\[f^\prime\left( \theta \right) = \left( {\cot \theta } \right)^\prime = - \frac{1}{{{{\sin }^2}\theta }}.\]
Substitute \({f\left( \theta \right)}\) and \({f^\prime\left( \theta \right)}\) into the expression for the derivative:
\[\frac{{dy}}{{dx}} = \frac{{\left( { - \frac{1}{{{{\sin }^2}\theta }}} \right) \cdot \sin \theta + \frac{{\cos \theta }}{{\sin \theta }} \cdot \cos \theta }}{{\left( { - \frac{1}{{{{\sin }^2}\theta }}} \right) \cdot \cos \theta - \frac{{\cos \theta }}{{\sin \theta }} \cdot \sin \theta }} = \frac{{ - \frac{1}{{\sin \theta }} + \frac{{{{\cos }^2}\theta }}{{\sin \theta }}}}{{ - \frac{{\cos \theta }}{{{{\sin }^2}\theta }} - \cos \theta }} = \frac{{\frac{1}{{\sin \theta }}\left( {1 - {{\cos }^2}\theta } \right)}}{{\frac{{\cos \theta }}{{{{\sin }^2}\theta }}\left( {1 + {{\sin }^2}\theta } \right)}} = \frac{{\frac{1}{{\sin \theta }} \cdot {{\sin }^2}\theta }}{{\frac{{\cos \theta }}{{{{\sin }^2}\theta }}\left( {1 + {{\sin }^2}\theta } \right)}} = \frac{{{{\sin }^2}\theta \cdot \sin \theta }}{{\cos \theta \left( {1 + {{\sin }^2}\theta } \right)}} = \frac{{{{\sin }^3}\theta }}{{\cos \theta \left( {1 + {{\sin }^2}\theta } \right)}}.\]
Calculate the value of the derivative at \(\theta = \frac{\pi }{6}:\)
\[\frac{{dy}}{{dx}}\left( {\theta = \frac{\pi }{6}} \right) = \frac{{{{\sin }^3}\frac{\pi }{6}}}{{\cos \frac{\pi }{6}\left( {1 + {{\sin }^2}\frac{\pi }{6}} \right)}} = \frac{{{{\left( {\frac{1}{2}} \right)}^3}}}{{\frac{{\sqrt 3 }}{2}\left( {1 + {{\left( {\frac{1}{2}} \right)}^2}} \right)}} = \frac{{\frac{1}{8}}}{{\frac{{\sqrt 3 }}{2}\left( {1 + \frac{1}{4}} \right)}} = \frac{{\frac{1}{8}}}{{\frac{{\sqrt 3 }}{2} \cdot \frac{5}{4}}} = \frac{{\frac{1}{8}}}{{\frac{{5\sqrt 3 }}{8}}} = \frac{1}{{5\sqrt 3 }} = \frac{{\sqrt 3 }}{{15}}.\]
Example 16.
Find the derivative \(\frac{{dy}}{{dx}}\) of the polar function \(r = \sec \left( {2\theta } \right)\) at \({\theta = \frac{\pi }{4}}.\)
Solution.
We use the formula
\[\frac{{dy}}{{dx}} = \frac{{f^\prime\left( \theta \right)\sin \theta + f\left( \theta \right)\cos \theta }}{{f^\prime\left( \theta \right)\cos \theta - f\left( \theta \right)\sin \theta }}.\]
As \(f\left( \theta \right) = \sec \left( {2\theta } \right) = \frac{1}{{\cos \left( {2\theta } \right)}},\) we have
\[f^\prime\left( \theta \right) = \left( {\frac{1}{{\cos \left( {2\theta } \right)}}} \right)^\prime = - \frac{1}{{{{\cos }^2}\left( {2\theta } \right)}} \cdot \left( {\cos \left( {2\theta } \right)} \right)^\prime = \frac{{2\sin \left( {2\theta } \right)}}{{{{\cos }^2}\left( {2\theta } \right)}}.\]
This yields
\[\frac{{dy}}{{dx}} = \frac{{\frac{{2\sin \left( {2\theta } \right)}}{{{{\cos }^2}\left( {2\theta } \right)}} \cdot \sin \theta + \frac{1}{{\cos \left( {2\theta } \right)}} \cdot \cos \theta }}{{\frac{{2\sin \left( {2\theta } \right)}}{{{{\cos }^2}\left( {2\theta } \right)}} \cdot \cos \theta - \frac{1}{{\cos \left( {2\theta } \right)}} \cdot \sin \theta }} = \frac{{\frac{{2\sin \left( {2\theta } \right)\sin \theta + \cos \left( {2\theta } \right)\cos \theta }}{{{{\cos }^2}\left( {2\theta } \right)}}}}{{\frac{{2\sin \left( {2\theta } \right)\cos \theta - \cos \left( {2\theta } \right)\sin \theta }}{{{{\cos }^2}\left( {2\theta } \right)}}}} = \frac{{2\sin \left( {2\theta } \right)\sin \theta + \cos \left( {2\theta } \right)\cos \theta }}{{2\sin \left( {2\theta } \right)\cos \theta - \cos \left( {2\theta } \right)\sin \theta }}.\]
Apply the double angle trig identities
\[\sin \left( {2\theta } \right) = 2\sin \theta \cos \theta ,\;\;\cos \left( {2\theta } \right) = {\cos ^2}\theta - {\sin ^2}\theta .\]
Hence
\[\frac{{dy}}{{dx}} = \frac{{4\,{{\sin }^2}\theta \cos \theta + {{\cos }^3}\theta - {{\sin }^2}\theta \cos \theta }}{{4\sin \theta {{\cos }^2}\theta - {{\cos }^2}\theta \sin \theta + {{\sin }^3}\theta }} = \frac{{3\,{{\sin }^2}\theta \cos \theta + {{\cos }^3}\theta }}{{3\,{{\cos }^2}\theta \sin \theta + {{\sin }^3}\theta }}.\]
At the point where \({\theta = \frac{\pi }{4}},\) the derivative is equal to
\[\frac{{dy}}{{dx}}\left( {\theta = \frac{\pi }{4}} \right) = \frac{{3\,{{\sin }^2}\frac{\pi }{4}\cos \frac{\pi }{4} + {{\cos }^3}\frac{\pi }{4}}}{{3\,{{\cos }^2}\frac{\pi }{4}\sin \frac{\pi }{4} + {{\sin }^3}\frac{\pi }{4}}} = \frac{{3 \cdot {{\left( {\frac{{\sqrt 2 }}{2}} \right)}^2} \cdot \frac{{\sqrt 2 }}{2} + {{\left( {\frac{{\sqrt 2 }}{2}} \right)}^3}}}{{3 \cdot {{\left( {\frac{{\sqrt 2 }}{2}} \right)}^2} \cdot \frac{{\sqrt 2 }}{2} + {{\left( {\frac{{\sqrt 2 }}{2}} \right)}^3}}} = 1.\]
Example 17.
The golden spiral is defined by the polar equation \(r = {\varphi ^{\frac{{2\theta }}{\pi }}},\) where \(\varphi = \frac{{1 + \sqrt 5 }}{2} \approx 1.618\) is the golden ratio. Find the angle \(\theta\) at which the tangent line to the curve is horizontal.
Solution.
Figure 14. As \(f\left( \theta \right) = {\varphi ^{\frac{{2\theta }}{\pi }}},\) we have
\[f^\prime\left( \theta \right) = \left( {{\varphi ^{\frac{{2\theta }}{\pi }}}} \right)^\prime = \frac{2}{\pi }{\varphi ^{\frac{{2\theta }}{\pi }}}\ln \varphi.\]
Write the derivative \(\frac{{dy}}{{dx}}\) of the polar function:
\[\frac{{dy}}{{dx}} = \frac{{f^\prime\left( \theta \right)\sin \theta + f\left( \theta \right)\cos \theta }}{{f^\prime\left( \theta \right)\cos \theta - f\left( \theta \right)\sin \theta }} = \frac{{\frac{2}{\pi }{\varphi ^{\frac{{2\theta }}{\pi }}}\ln \varphi \sin \theta + {\varphi ^{\frac{{2\theta }}{\pi }}}\cos \theta }}{{\frac{2}{\pi }{\varphi ^{\frac{{2\theta }}{\pi }}}\ln \varphi \cos \theta - {\varphi ^{\frac{{2\theta }}{\pi }}}\sin \theta }} = \frac{{\frac{2}{\pi }\ln \varphi \sin \theta + \cos \theta }}{{\frac{2}{\pi }\ln \varphi \cos \theta - \sin \theta }} = \frac{{\frac{2}{\pi }\ln \varphi \tan \theta + 1}}{{\frac{2}{\pi }\ln \varphi - \tan \theta }} = \frac{{2\ln \varphi \tan \theta + \pi }}{{2\ln \varphi - \pi \tan \theta }}.\]
Determine the angle \(\theta\) at which the slope of the tangent line is zero:
\[\frac{{dy}}{{dx}} = 0,\;\; \Rightarrow \frac{{2\ln \varphi \tan \theta + \pi }}{{2\ln \varphi - \pi \tan \theta }} = 0,\;\; \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{2\ln \varphi \tan \theta + \pi = 0}\\
{2\ln \varphi - \pi \tan \theta \ne 0}
\end{array}} \right.,\;\; \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{\tan \theta = - \frac{\pi }{{2\ln \varphi }}}\\
{\tan \theta \ne \frac{{2\ln \varphi }}{\pi }}
\end{array}} \right.,\;\; \Rightarrow \theta = \arctan \left( { - \frac{\pi }{{2\ln \varphi }}} \right).\]
Let's evaluate this angle:
\[ - \frac{\pi }{{2\ln \varphi }} = - \frac{\pi }{{2\ln \frac{{1 + \sqrt 5 }}{2}}} \approx - 3.264\]
Hence
\[\theta = \arctan \left( { - \frac{\pi }{{2\ln \varphi }}} \right) \approx \arctan \left( { - 3.264} \right) = 107^\circ.\]