Differential Equations

First Order Equations

1st Order Diff Equations Logo

Barometric Formula

In this section we derive how the gas pressure P depends on the height over sea level h in the gravitational field of Earth.

If we take an arbitrary gas column with intersection area S and height h, then the weight of this column is given by

\[F = mg = \rho gV = \rho ghS,\]

where ρ is the gas density. Then the gas pressure is expressed by the following formula:

\[P = \frac{F}{S} = \frac{{\rho gh\cancel{S}}}{\cancel{S}} = \rho gh.\]

Now imagine such a column in the atmosphere and separate a thin layer of air with the height \(dh\) (Figure \(1\)).

A column in the atmosphere and a thin layer of air with the height dh
Figure 1.

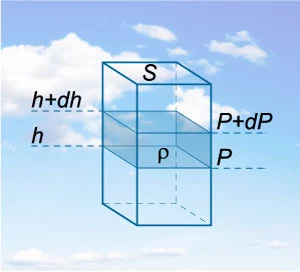
It's clear that such a layer causes the pressure change by the value of

\[dP = - \rho gdh.\]

We have put the minus sign because the pressure must decrease as the altitude increases.

Considering atmospheric air as an ideal gas, we can use the ideal gas law to express the density \(\rho\) through pressure \(P:\)

\[PV = \frac{m}{M}RT,\;\; \Rightarrow P = \frac{m}{{VM}}RT = \frac{\rho }{M}RT. \]

Here \(T\) is the absolute temperature, \(R\) is the universal gas constant equal to \(8.314\,{\frac{\text{J}}{K \cdot \text{mol}}},\) \(M\) is the molar mass, which is for air equal to \(0.029\,{\frac{\text{kg}}{\text{mol}}}.\) It follows from here that the density is given by the formula

\[\rho = \frac{{MP}}{{RT}}.\]

Putting this into the differential relation for \(dP\) gives:

\[dP = - \rho gdh = - \frac{{MP}}{{RT}}gdh,\;\; \Rightarrow \frac{{dP}}{P} = - \frac{{Mg}}{{RT}}dh.\]

We obtain a differential equation describing the gas pressure \(P\) as a function of the altitude \(h.\) Integrating gives the equation:

\[\int {\frac{{dP}}{P}} = - \int {\frac{{Mg}}{{RT}}dh} ,\;\; \Rightarrow \ln P = - \frac{{Mg}}{{RT}}h + \ln C.\]

Getting rid of the logarithms, we obtain the so-called barometric formula

\[P = C\exp \left( { - \frac{{Mg}}{{RT}}h} \right).\]

The constant of integration \(C\) can be determined from the initial condition \(P\left( {h = 0} \right) = {P_0},\) where \({P_0}\) is the average sea level atmospheric pressure.

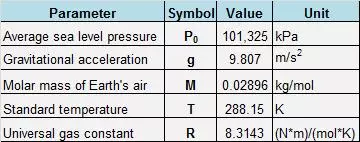
Standard atmosphere conditions
Figure 2.

Note: The standard temperature \(T = 288.15\,\text{K}\) corresponds to the International Standard Atmosphere (ISA) model.

Thus, dependency of the barometric pressure on the altitude is given by the formula

\[P = {P_0}\exp \left( { - \frac{{Mg}}{{RT}}h} \right).\]

Substituting the known constant values (see Figure \(2\)), we find that the dependence \(P\left( h \right)\) (in kilopascals) is expressed by the formula:

\[P\left( h \right) = 101.325 \cdot \exp \left( { - \frac{{0.02896 \cdot 9.807}}{{8.3143 \cdot 288.15}}h} \right) = 101.325\exp \left( { - 0.00012\,h} \right)\; \left[\text{kPa} \right],\]

where the height \(h\) above sea level is expressed in meters.

If the pressure is given in millimeters of mercury \(\left( \text{mmHg} \right),\) the barometric formula is written in the form:

\[P\left( h \right) = 760\exp \left( { - 0.00012\,h} \right)\; \left[ \text{mmHg} \right].\]

In case when the height \(h\) is given in feet, and pressure in inches of mercury \(\left( \text{inHg} \right),\) this formula is written as

\[P\left( h \right) = 29.92\exp \left( { - 0.0000366\,h} \right)\; \left[ \text{inHg} \right].\]

The barometric formula is often used for estimating the air pressure under different conditions, although it gives slightly higher values compared with the real ones.

Solved Problems

Example 1.

Determine at what altitude the air pressure is twice less than on the sea level?

Solution.

To estimate the altitude, we use the barometric formula

\[P\left( h \right) = {P_0}\exp \left( { - 0.00012\,h} \right).\]

When \(h = 0\), the pressure \(P\left( h \right)\) is equal to the average atmospheric sea level pressure \({P_0}.\) At a certain altitude \(H\), the pressure is twice less:

\[P\left( H \right) = \frac{{{P_0}}}{2} = {P_0}\exp \left( { - 0.00012\,H} \right).\]

It follows from here that

\[\exp \left( { - 0.00012\,H} \right) = \frac{1}{2}.\]

Taking logarithms of both sides, we find the altitude \(H:\)

\[\ln \frac{1}{2} = - 0.00012\,H,\;\; \Rightarrow \ln 2 = 0.00012\,H,\;\; \Rightarrow H = \frac{{\ln 2}}{{0.00012}} \approx 5780\,\text{m}.\]

Example 2.

Find the air pressure in a mine at a depth of \(1\,\text{km}\) at the temperature of \(40\) degrees Celsius.

Solution.

The air pressure in the mine can be estimated using the general barometric formula:

\[P = {P_0}\exp \left( { - \frac{{Mg}}{{RT}}h} \right).\]

We substitute the following values into the formula: \(h = - 1000\,\text{m}\) (the sign is minus because the mine is under sea level); \(T = 40 + 273.15 = 313.15\,\text{K}.\) The remaining parameters are standard: \(M = 0.02896\,\frac{\text{kg}}{\text{mol}},\) \(R = 8.3143\,\frac{\text{N}\cdot\text{m}}{\text{mol}\cdot\text{K}},\) \(g = 9.807\,\frac{\text{m}}{\text{s}^2}.\)

After simple calculations we find:

\[P = {P_0}\exp \left( { - \frac{{Mg}}{{RT}}h} \right) = {P_0}\exp \left[ { - \frac{{0.02896 \cdot 9.807}}{{8.3143 \cdot 313.15}}\left( { - 1000} \right)} \right] \approx {P_0}\exp \left( {0.109} \right) \approx 1.115{P_0}.\]

Since the atmospheric sea level pressure is \({P_0} = 760\;\text{mmHg},\) the air pressure in the mine will be \(848\;\text{mmHg},\) that is about \(12\) percent greater than at sea level.